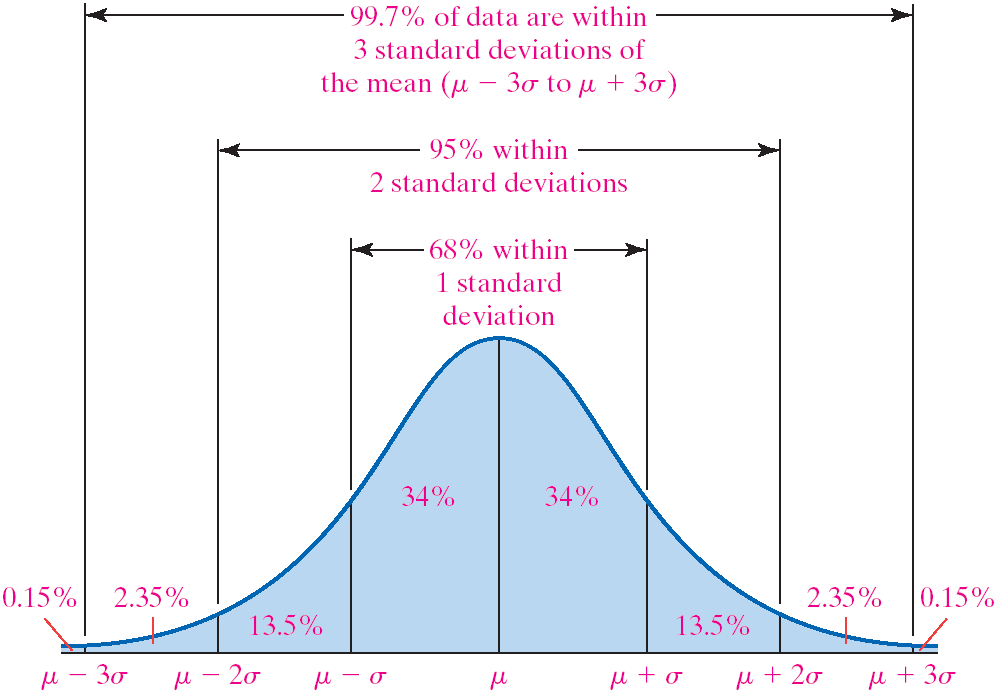
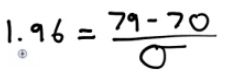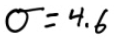The Empirical Rule

0.15% 2.35% 99.7% of data are within 3 standard deviations of the mean (11 — to + 3(T) 95% within 2 standard deviations 68% within I standard deviation 34 13.5% 2.35% 13.5% 0.15%

Z Scores (Standardized Score)

  • How many standard deviations away from the mean your value x is

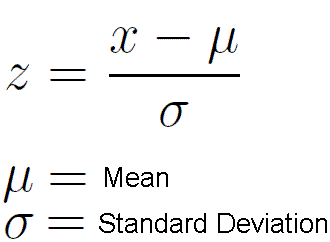
    z Mean = Standard Deviation

Using the Normal Table

Probability Table entry for z is the probability lying below z. T able A Standard normal probabilities -3.4 -3.3 -3.2 -3.1 -3.0 -2.9 -2.8 -2.7 -2.6 -2.5 -2.4 -2.3 -2.2 -2.1 -2.0 -1.9 -1.8 -1.7 —1.6 -1.5 -1.4 -1.3 -1.2 -1.1 -1.0 -0.9 -0.8 -0.7 —0.6 -0.5 -0.4 -0.3 -0.2 -0.1 -0.0 .00 0010 .0013 .0019 .0035 .0047 .0062 .0082 .0107 .0139 .0179 .0228 .0287 .0359 .0548 .0808 .1151 .1357 .1587 .1841 .2119 .2420 .2743 .3085 .3821 .4207 .4602 .01 .0003 .0005 .0013 .0018 .0025 .0045 .0104 .0136 .0174 .0222 .0281 .0351 .0436 .0537 .0655 .0793 .0951 .1131 .1335 .1562 .1814 .2090 .2389 .2709 .3050 .3409 .3783 .4168 .4562 .496() .02 .0003 .0005 .0013 .0018 .0024 .0033 .0059 .0078 .0102 .0132 .0170 .0217 .0274 .0427 .0526 .0643 .0778 .0934 .1112 .1314 .1539 .1788 .2061 .2358 .2676 .3015 .3372 .3745 .4129 .4522 .4920 .03 0003 0006 0009 0012 0017 0032 0057 0075 0099 .0129 .0166 0212 0336 0418 .0516 0630 .0764 0918 .1093 .1292 .1515 .1762 .2033 .2327 .2981 .3336 .3707 .4090 .4483 .4880 .04 .0012 .0016 .0023 .0031 .0041 .0055 .0073 .0125 .0162 .0207 .0262 .0329 .0505 .0618 .0749 .0901 .1075 .1271 .1492 .1736 .2005 .2296 .2611 .2946 .3300 .3669 .4052 .4443 .4840 .05 .0011 .0016 .0030 .0054 .0071 .0122 .0158 .0202 .0256 .0322 0401 .0495 .0606 .0735 .0885 .1056 .1251 .1469 .1711 .1977 .2266 .2578 .2912 .3264 .3632 .4013 .4801 .06 .0003 .00(M .0006 .0008 .0011 .0015 .0021 .0029 .0039 .0052 .0069 .0091 .0119 .0154 .0197 .0250 .0314 .0392 .0485 .0594 .0721 .0869 .1038 .1230 .1446 .1685 .1949 .2236 .2877 .3228 .3594 .3974 .4364 .4761 .07 .0003 .0005 .0008 .00\]1 .0015 .0021 .0028 .0038 .0051 .0068 .0089 .0116 .0150 .0192 .0244 .0307 .0384 .0475 .0582 .0708 .0853 .1020 .1210 .1423 .1660 .1922 .2514 .2843 .3192 .3557 .3936 .4325 .4721 .08 .0003 .0004 .0005 .0007 .0010 0014 0020 0027 0037 0049 .0066 .0087 .0113 .0146 .0188 0239 0301 0375 0465 0571 .0694 .0838 .1003 .1 190 .1401 .1635 .1894 .2177 .2483 .2810 .3156 .3520 .3897 .4286 .4681 .09 .0002 .0003 .0005 .0007 .0010 .0014 .0019 .0026 .0036 .0048 .0064 .0084 .0110 .0143 .0183 .0233 .0294 .0367 .0455 .0559 .0681 .0823 .0985 .1170 .1379 .1611 .1867 .2148 .2451 .2776 .3121 .3483 .3859 .4247 .4641

Table entry for z is the probability lying below z. T able A (Continued) 0.0 0.1 0.2 0.3 0.4 0.5 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 3.0 3.1 3.2 3.3 3.4 .00 .5000 .5398 .5793 .6179 .6554 .6915 .7580 .7881 .8159 .8413 .8643 .8849 .9032 .9192 .9332 .9452 .9554 .9641 .9713 .9772 .9821 .9861 .9893 .9918 .9938 .9953 .9965 .9974 .9981 .9987 .9990 .9993 .9995 .9997 .01 .5040 .5438 .5832 .6217 .6591 .6950 .7291 .7611 .7910 .8186 .8438 .8665 .8869 .9049 .9207 .9345 .9564 .9649 9719 .9778 .9826 .9864 .9896 .9920 .9955 .9966 .9975 .9982 .9987 .9991 .9993 .9995 .9997 .02 .5080 .5478 .5871 .6255 .6628 .6985 .7324 .7642 .7939 .8212 .8461 -8686 .8888 .9066 .9222 .9357 .9474 .9573 .9656 .9726 .9783 .9830 .9868 .9898 .9922 .9941 .9956 .9967 .9976 .9982 .9987 .9991 .9994 .9995 .9997 .03 .5120 .5517 .5910 .6293 .7019 .7357 .7673 .7967 .8238 .8485 .8708 .8907 .9082 .9236 .9370 .9484 .9582 .9664 .9732 .9788 .9834 .9871 .9901 .9925 .9943 .9957 .9968 .9983 .9988 .9991 .9996 Probability .04 .5160 .5557 .5948 .6331 .6700 .7054 .7389 .7704 .7995 .8508 .8729 .8925 .9099 .9251 .9382 .9495 .9591 .9671 .9738 .9793 .9838 .9875 .9927 .9945 .9959 .9969 .9977 .9984 .9988 .9992 .9994 .9996 .9997 .05 .5199 .5596 .5987 .6368 .6736 .7088 .7422 .7734 .8023 .8289 .8531 .8749 .8944 .9115 .9265 .9394 .9505 .9599 .9678 .9744 .9798 .9842 .9878 .9929 .9970 .9978 .9984 .9989 .9997 .06 .5239 .5636 .6026 .6772 .7123 .7454 .7764 .8051 .8315 .8554 .8770 .8962 .9131 .9406 .9515 .9608 .9686 .9750 .9846 .9881 .9909 .9931 .9948 .9961 .9971 .9979 .9985 .9989 .9992 .9994 .9996 .9997 .07 .5279 .5675 6443 .6808 .7157 .7486 .7794 .8078 .8340 .8577 .8790 .8980 .9147 .9292 .9418 .9525 .9616 .9693 .9756 .9808 .9850 .9884 .9911 .9932 .9949 .9962 .9972 .9979 .9985 .9989 .9992 .9995 .9996 .9997 .08 .5319 .5714 .6103 .6480 .6844 .7190 .7517 .7823 .8106 .8365 .8599 .8810 .8997 .9162 .9306 .9429 .9535 .9625 .9699 .9761 .9812 .9854 .9887 .9913 .9934 .9951 .9963 .9973 .9980 .9986 .9990 .9993 .9995 g 996 g 997 .09 .5359 .5753 .6141 .6517 .6879 .7224 .7549 .7852 .8133 .8389 .8621 .8830 .9015 .9177 .9319 .9441 .9545 .9633 .9706 .9767 .9817 .9857 .9890 .9916 .9936 .9952 .9964 .9974 .9981 .9986 .9990 .9993 .9995 g 997 .9998

Practice Questions

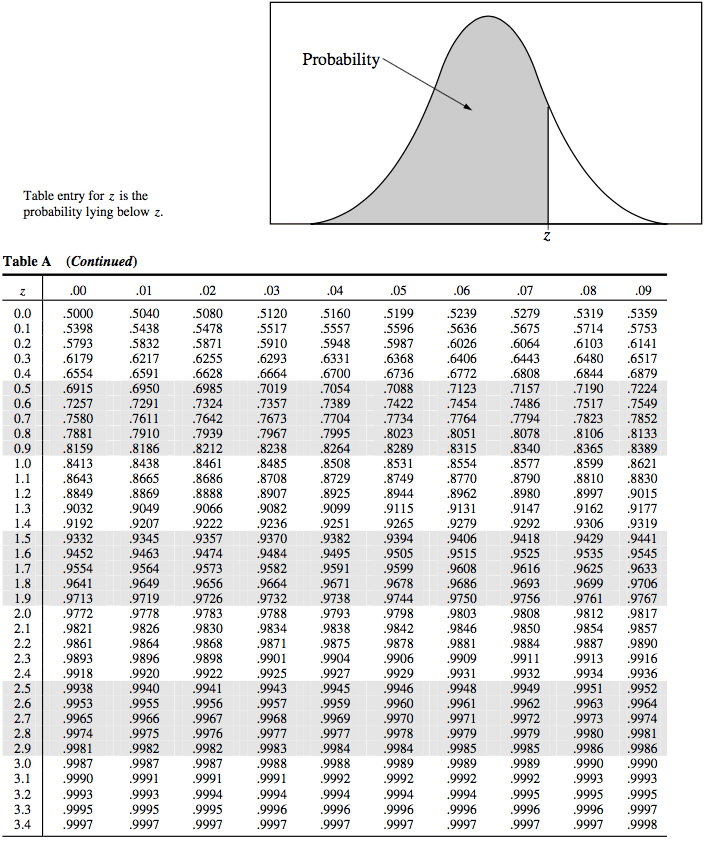
  1. A study of college freshmen's study habits found that the time (in hours) that college freshmen use to study each week follows a normal distribution with a mean of 7.2 hours and a standard deviation of 5.3 hours

  • How many hours do the students who study in the top 15% spend studying?

  • The middle 68%?

    • Top 15%: 12.5 hours

    • Middle 68%: 1.9 hours to 12.5 hours

    Âli VI 74,6

  1. Suppose that the weight of navel oranges is normally distributed with mean of 8 ounces, and standard deviation of 1.3 ounces. And the weights of Valencia oranges is normally distributed with mean of 9 ounces, and standard deviation of 1.6 ounces

  • You grow a navel orange that weighs 9.5 ounces and a Valencia orange that weight 10.5 ounces, which should you enter in the giant fruit contest?

    C:\\6432CA65\\FE01530B-89BD-4F8B-A3E1-55F12080AD12\_files\\image144.png

  • Z score for navel orange = (9.5-8)/1.3 = 1.1538

  • Z score for Valencia orange = (10.5-9)/1.6 = 0.9375

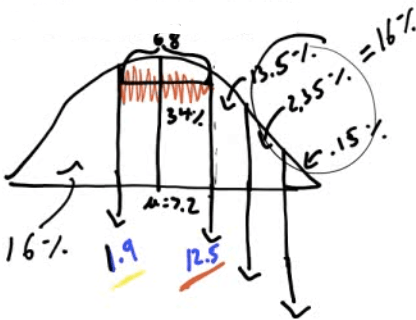
  • The weights of newborn children in the United States vary according to the Normal Distribution with mean 7.5 pounds and standard deviation 1.25 pounds.

  • What is the probability that a baby chosen at random weighs less than 5.5 pounds at birth?

    1. Draw a sketch

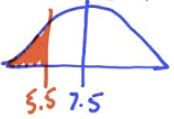
    C:\\6432CA65\\FE01530B-89BD-4F8B-A3E1-55F12080AD12\_files\\image145.png

  1. Calculate Z score

    - 7.s 1-25 -2

  2. Look up probability on the normal table

    es€o•o

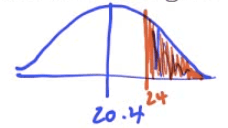
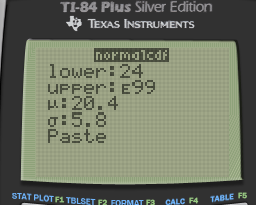
  3. The composite score of students on the ACT college entrance examination in a recent year had a Normal distribution with mean of 20.4 and standard deviation of 5.8

  • What is the probability that a randomly chosen students scored 24 or higher on the ACT?

    1. Sketch

    C:\\6432CA65\\FE01530B-89BD-4F8B-A3E1-55F12080AD12\_files\\image148.png

  1. 2ND + VARS (DISTR) ➡️ 2: normalcdf

    Tl-B4 mus Ed-tjcn TEXAS CIRHW 1 : normalFdf( ænor•mal s: invNorm( 4: inwT( 5: tpdf( 6 : tc.df(. STAT OT 'A" E

  2. Normalcdf(lower, upper, mean, standard deviation)

    Tl-84 Pius Silver Ecfitjm TEXAS INSTRUMENTS STAT Is

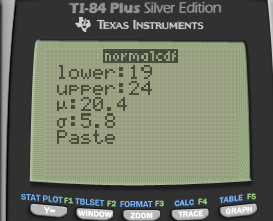
    • What is the probability that a randomly chosen student scored between a 19 and a 24 on the ACT?

    Tl-B4 Pius Silver E lower: 13 upper : 24 g: 23.4 o:5.e Past.e

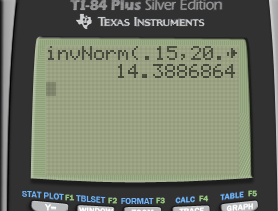
    • What score would someone in the 15th percentile have scored?

    • Sketch

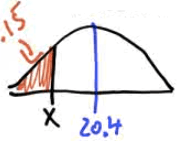
    C:\\6432CA65\\FE01530B-89BD-4F8B-A3E1-55F12080AD12\_files\\image152.png

  3. Find the z value on the normal table

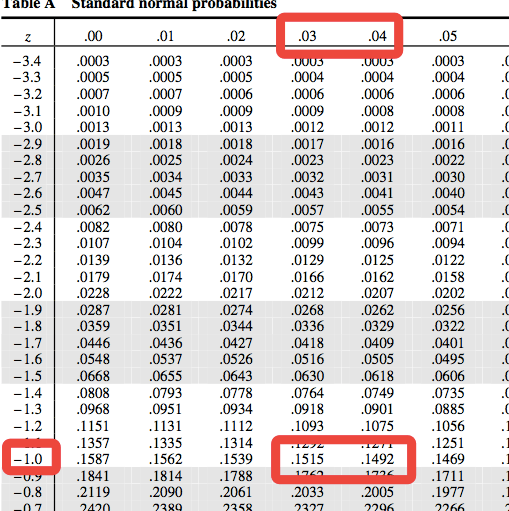
    3.4 3.3 3.2 3.1 3.0 2.9 2.8 2.7 2.6 2.5 2.4 2.3 2.2 2.1 2.0 1.9 1.8 1.7 1.6 1.5 1.3 1.2 -1.0 -0.8 .00 .0003 .0005 .0007 .0010 .0013 .0019 .0026 .0035 .0047 .0062 .0082 .0107 .0139 .0179 .0228 .0287 .0359 .0446 .0548 .0668 .0808 .0968 .1151 .1357 .1587 .1841 .2119 .01 .0013 .0018 .0025 .0034 .0060 .0080 .0104 .0136 .0174 .0222 .0281 .0351 .0436 .0537 .0655 .0793 .0951 .1131 .1335 .1562 .1814 .2090 .02 .0003 .0005 .0013 .0018 .0033 .0059 .0078 .0102 .0132 .0170 .0217 .0274 .0344 .0427 .0526 .0643 .0778 .0934 .11 12 .1314 .1539 .1788 .2061 .03 .0004 .0006 .0009 .0012 .0017 .0023 .0032 .0057 .0075 .0099 .0129 .0166 .0212 .0268 .0336 .0418 .0516 .0630 .0764 .0918 .1093 .1515 .2033 .04 .0004 .0006 .0008 .0012 .0016 .0023 .0031 .0041 .0055 .0073 .0096 .0125 .0162 .0207 .0262 .0329 .0409 .0505 .0618 .0749 .0901 .1075 .1492 .2005 .05 .0003 .0008 .0011 .0016 .0022 .0030 .0071 .0122 .0158 .0256 .0322 .0401 .0495 .0606 .0735 .0885 .1056 .1251 .1469 .1711 .1977

    Z≈-1.035

  4. Solve for x

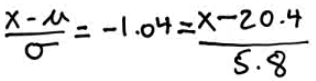
    C:\\6432CA65\\FE01530B-89BD-4F8B-A3E1-55F12080AD12\_files\\image154.png

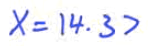
    C:\\6432CA65\\FE01530B-89BD-4F8B-A3E1-55F12080AD12\_files\\image155.png

  5. Calculator: invNorm(area, mean, standard deviation)

    TEXAS INSTRUMENTS eag:.e FORMAT n

    ![ф TEns [NSTRUMENTS 14 „ гоямдтп си: ТАТЕ ](./media/image157.png)

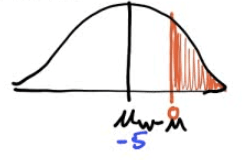
  6. Suppose that the mean height of men is 70 inches with a standard deviation of 3 inches. And suppose that the mean height for women is 65 inches with a standard deviation of 2.5 inches

  • If the heights of men and women are Normally distributed, find the probability that a randomly selected woman is taller than a randomly selected man.

    1. Sketch

    C:\\6432CA65\\FE01530B-89BD-4F8B-A3E1-55F12080AD12\_files\\image158.png

  1. Find the necessary information
Mean SD
Men 70 3
Women 65 2.5
W-M 65-70 = -5 Sqrt(3^2+2.5^2) = 3.9

  1. Calculate Z score

    (s-7-0 ?

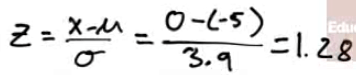
  2. Find the probability on the table and subtract that from 1

    1-0.9015 = 0.0985 = 9.85%

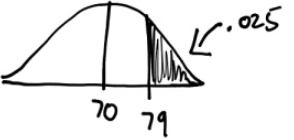
    • Suppose that the height (X) in inches, of adult men is a normal random variable with mean of 70 inches. If P (X>79) = 0.025

    • What is the standard deviation of this random normal variable?

    • Sketch

    C:\\6432CA65\\FE01530B-89BD-4F8B-A3E1-55F12080AD12\_files\\image160.png

  3. Find the z score on the calculator: invNorm(area)

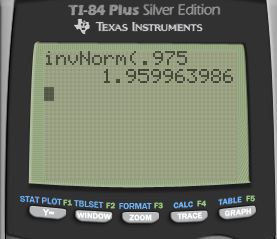
    ![ТИ-84 PIus S'tver Editj(n ф TEns [NSTRUMENTS гоямдта ](./media/image161.png)

  4. Solve for SD

    C:\\6432CA65\\FE01530B-89BD-4F8B-A3E1-55F12080AD12\_files\\image162.png

    C:\\6432CA65\\FE01530B-89BD-4F8B-A3E1-55F12080AD12\_files\\image163.png

results matching ""

    No results matching ""